Scientific Achievement
Reconciles two classical model descriptions of membrane transport for swollen non-porous membrane using the Fluid-solid model, a unified mechanical framework to approach solvent transport.
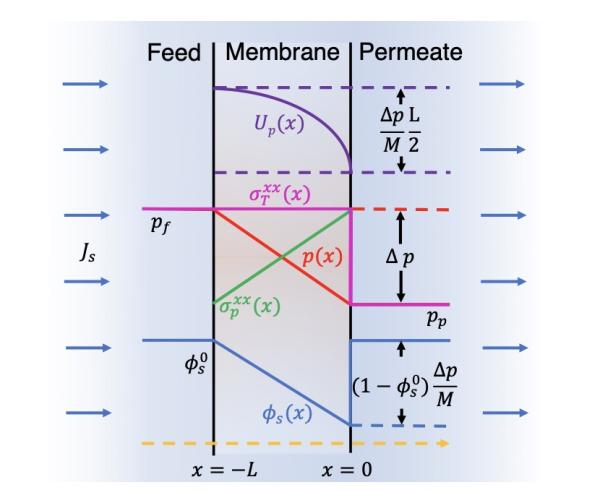
Image: Steady state network displacement (U(p)), fluid pressure (p), polymer stress (σ(p)), and solvent volume fraction (ɸ(s)) profiles across solvent swollen non-porous membrane bound to a permeable support at the permeate boundary. Compression of the polymer network is dictated by the imposed pressure drop, Δp, and the longitudinal modulus of uni-axial compression, M.
Significance and Impact
The Fluid-solid model identifies the longitudinal elastic modulus as a key parameter that impacts membrane performance while clarifying recent reverse osmosis measurements, providing a predictive and mechanistic basis for empirical high-pressure limiting flux phenomena, in agreement with classic measurements, and laying a framework to treat non-porous but mechanically heterogeneous membrane materials.
Research Details
- Adapted the fluid-solid model, a gel dynamics framework to describe the mechanical of swollen non-porous membranes.
- Reconciled the Solution-diffusion and pore flow descriptions of this system.
- Predicts the non-linear high pressure limiting flux relation.
Notes
Two models describe solvent transport through swollen, nonporous membranes. The pore-flow model, based on fluid mechanics, works for porous membranes, whereas the solution-diffusion model invokes molecular diffusion to treat non-porous membranes. Both approaches make valid arguments for swollen polymer membranes, but disagree in their predictions of intra-membrane pressure and concentration profiles. Using a fluid-solid model that treats the solvent and membrane matrix as separate phases, we show both classical models to be valid, to represent complementary approaches to the same phenomenon, and to make identical predictions. The fluid-solid model clarifies recent reverse osmosis measurements, provides a predictive and mechanistic basis for empirical high-pressure limiting flux phenomena, in quantitative agreement with classic measurements, and gives a framework to treat non-porous but mechanically heterogeneous membrane materials.
Most importantly the model identifies the longitudinal osmotic modulus, the elastic modulus of uni-axial compression as the key mechanical parameter that dictates membrane compression during transport, and in turn membrane performance.
Acknowledgements
Images courtesy of Mostafa Nasser (Fig. 1A) and Alexander Bridge (Fig. 1B,1C,1D). Funding: This work was supported as part of the Center for Materials for Water and Energy Systems (M-WET), an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0019272. Authors contributions: Varun H. Hegde: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Writing - original draft, Writing - review and editing. Michael F. Doherty: Conceptualization, Writing - Review and Editing, Supervision, Project administration, Funding acquisition. Todd M. Squires: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Writing - original draft, Writing - review and editing, Supervision, Project administration, Funding acquisition. Competing interests: None declared Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper or the Supplementary Materials.
Reference
Varun H. Hegde, Michael F. Doherty, and Todd M. Squires, "A two-phase model that unifies and extends the classical models of membrane transport," Science, in press.

