GAP C, Project 1: Design and Preparation of Isoporous Separation Membranes
GAP C research will leverage our early experience in performing the SNIPS process with PS-b-P4VP and related systems (cf. Fig. 4.2) towards the reproducible fabrication of isoporous asymmetric membranes from UMCP materials. Experimental efforts will be directed at understanding and harnessing the nonequilibrium phenomena that will enable the manufacture of isoporous membranes with tunable pore size and size distribution. New UMCP copolymers will be characterized for solution phase ordering via X-ray scattering to narrow the casting solution design space to solvents best suited for inducing self-assembly (Su). UMCP variants capable of forming isoporous asymmetric membranes will undergo further characterization of thermomechanical properties via tensile testing, dynamic mechanical analysis, and thermogravimetric analysis of dense films (Sanoja) to inform synthetic efforts aimed at improving material strength/toughness and thermal stability (Lynd). Isoporous UMCP membrane structures will be identified and characterized via electron microscopy, and X-ray scattering. Their separation performance, namely pure water permeance, molecular weight cutoff, solute rejection, and fouling behavior, will also be measured in the IF (Freeman).
The experimental program on SNIPS will leverage a parallel theoretical and computational effort to develop and exploit models of the dry evaporation and wet immersion steps of SNIPS. Phase field models will be constructed (Fredrickson, Ganesan) based on multi-component fluctuating diffusion equations (Model B dynamics) for the densities of solvent, non-solvent, co-solvent, and individual block species. The Rouse model is used to compute the Onsager mobility tensor in the dynamical equations. Structural arrest is described by the sigmoidal increase in local friction experienced by solvents and polymer segments when a glass transition threshold is crossed. Such a model produced realistic asymmetric membrane structures in prior NIPS simulations. Unlike that work, where the chemical potential gradients driving multicomponent diffusion were derived from a phenomenological Flory-Huggins-de Gennes free energy functional, the thermodynamic forces will be numerically computed using self-consistent field theory (SCFT). This approach embeds a rich thermodynamic basis for the model that has a molecular origin faithful to the multiblock polymer architectures deployed. The resulting dynamic SCFT framework (DSCFT) can capture both the macrophase and microphase separation processes involved in SNIPS.
Modeling of the dry and wet steps of SNIPS will occur sequentially. The dry evaporation protocol will follow previous work on modeling solvent evaporation from thin block copolymer films. Key variables to explore are the evaporation time, the solvent volatility, and the block selectivities towards solvent, cosolvent, and air. The morphological output from the dry evaporation step provides the initial condition for wet immersion, wherein the air phase is replaced by a non-solvent bath that is permitted to diffuse into the film and initiate macrophase separation. A preliminary example of the output from such a two-step simulation is shown in Fig. 4.3 for a symmetric (i.e., 𝑓A = 0.5) AB diblock copolymer in a film with a nonselective solvent S (equal Flory interaction parameters, 𝜒AS. = 𝜒BS.). In this simple two-dimensional example, the non-solvent is also non-selective for the A and B blocks (i.e., 𝜒AN = 𝜒BN). Fig. 4.3 reveals a skin layer with well-organized vertical diblock lamellae transitioning below into a membrane structure with solvent-filled macropores. Future investigations will extend to three dimensions, focus on the UMCP architecture, and include vitrification when the concentration of the matrix-forming block locally exceeds a glass transition threshold.
Since GAPS A and B will incorporate functional groups to impart selectivity to UMCP membranes via chemistry that can be implemented in either the porous or non-porous formats, the SNIPS/NIPS manufacturing process must be robust to these additional groups. Yet, we have found that the inclusion of a relatively small pendant group has a profound effect on the Flory interaction parameter87, potentially altering the thermodynamics of phase separation/membrane formation substantially. An important component of the modeling effort will be to establish a reliable method of estimating the Flory interaction parameters that are inputs to the dynamical theory and describe the pairwise interactions among polymer segments, solvents, co-solvents, and non-solvent. Because the chemical variations that will be explored in the project are wide-ranging, an in silico method that requires no experimental input will be pursued. Specifically, structure factors obtained from all-atom molecular dynamics (MD) simulations of short polymer blocks mixed with solvents or low molecular weight polymers will be fit to analytical random phase approximation (RPA) structure factors to extract 𝜒 parameters (Ganesan, Fredrickson). Although this procedure has precedent in the literature, we have recently discovered that substituting intramolecular scattering information obtained from the MD simulations for theoretical Debye functions yields much more accurate values of 𝜒.
The experimental and theoretical components of Project 1 will be closely coordinated, with theory informing experiment of the most promising polymer designs and choices of solvents, casting conditions, and with experiments providing a platform for validating the assumptions and parameters of the underlying models.
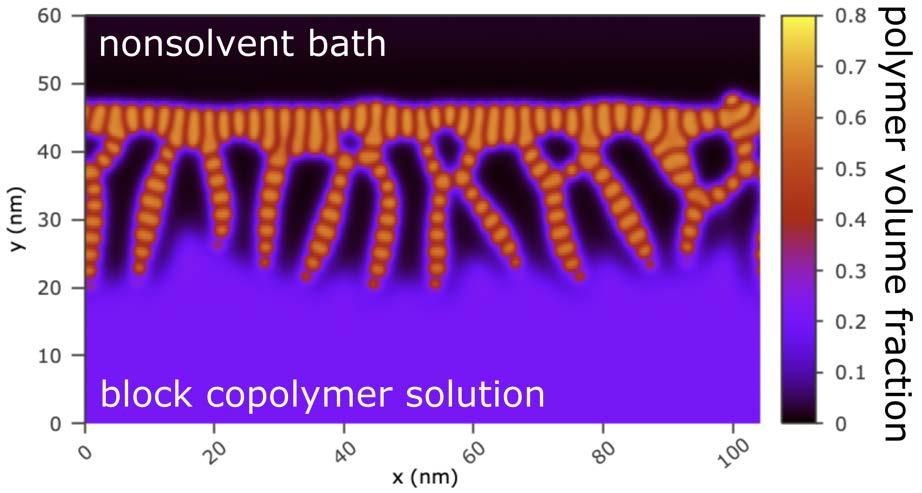
Fig. 4.3. Morphology obtained from dynamic SCFT simulation of mass transfer at an AB block copolymer solution/nonsolvent bath interface, for 𝑁 = 50, 𝑓A| = 0.5, 𝜒AB = 1, 𝜒AS. = 𝜒BS = 0.8, and 𝜒AN = 𝜒BN = 1.048. The initial volume fractions in the bulk of the polymer solution film are 𝜙P = 0.2 (polymer), 𝜙S = 0.7 (solvent), and 𝜙N = 0.1 (nonsolvent).

